Graph traversals in AQL

Syntax

There are two slightly different syntaxes for traversals in AQL, one for

• named graphs and another to
• specify a set of edge collections (anonymous graph).

Working with named graphs

[WITH vertexCollection1[, vertexCollection2[, ...vertexCollectionN]]]
FOR vertex[, edge[, path]]
  IN [min[..max]]
  OUTBOUND|INBOUND|ANY startVertex
  GRAPH graphName
  [PRUNE pruneCondition]
  [OPTIONS options]

• WITH: optional for single server instances, but required for graph traversals in a cluster.
  • collections (collection, repeatable): list of vertex collections that will be involved in the traversal
• FOR: emits up to three variables:
  • vertex (object): the current vertex in a traversal
  • edge (object, optional): the current edge in a traversal
  • path (object, optional): representation of the current path with two members:
    • vertices: an array of all vertices on this path
    • edges: an array of all edges on this path
• IN min..max: the minimal and maximal depth for the traversal:
  • min (number, optional): edges and vertices returned by this query will start at the traversal depth of min (thus edges and vertices below will not be returned). If not specified, it defaults to 1. The minimal possible value is 0.
  • max (number, optional): up to max length paths are traversed. If omitted, max defaults to min. Thus only the vertices and edges in the range of min are returned. max can not be specified without min.
• OUTBOUND|INBOUND|ANY: follow outgoing, incoming, or edges pointing in either direction in the traversal; Please note that this can’t be replaced by a bind parameter.
• startVertex (string|object): a vertex where the traversal will originate from. This can be specified in the form of an ID string or in the form of a document with the attribute _id. All other values will lead to a warning and an empty result. If the specified document does not exist, the result is empty as well and there is no warning.
• GRAPH graphName (string): the name identifying the named graph. Its vertex and edge collections will be looked up. Note that the graph name is like a regular string, hence it must be enclosed by quote marks.
• PRUNE condition (AQL condition, optional): A condition, like in a FILTER statement, which will be evaluated in every step of the traversal, as early as possible. The semantics of this condition is as follows:
  • If the condition evaluates to true this path will be considered as a result, it might still be post filtered or ignored due to depth constraints. However the search will not continue from this path, namely there will be no result having this path as a prefix. e.g.: Take the path: (A) -> (B) -> (C) starting at A and PRUNE on B will result in (A) and (A) -> (B) being valid paths, and (A) -> (B) -> (C) not returned, it got pruned on B.
  • If the condition evaluates to false we will continue our search beyond this path. There is only one PRUNE condition possible, but it can contain an arbitrary amount of AND or OR statements. Also note that you can use the output variables of this traversal in the PRUNE, as well as all variables defined before this Traversal statement.
• OPTIONS options (object, optional): used to modify the execution of the traversal. Only the following attributes have an effect, all others are ignored:
  • order (string): optionally specify which traversal algorithm to use
    • "bfs" – the traversal will be executed breadth-first. The results will first contain all vertices at depth 1, then all vertices at depth 2 and so on.
    • "dfs" (default) – the traversal will be executed depth-first. It will first return all paths from min depth to max depth for one vertex at depth 1, then for the next vertex at depth 1 and so on.
    • "weighted" - the traversal will be a weighted traversal (introduced in v3.8.0). Paths are enumerated with increasing cost. Also see weightAttribute and defaultWeight. A returned path has an additional attribute weight containing the cost of the path after every step. The order of paths having the same cost is non-deterministic. Negative weights are not supported and will abort the query with an error.
  • bfs (bool): deprecated, use order: "bfs" instead.
  • uniqueVertices (string): optionally ensure vertex uniqueness
    • "path" – it is guaranteed that there is no path returned with a duplicate vertex
    • "global" – it is guaranteed that each vertex is visited at most once during the traversal, no matter how many paths lead from the start vertex to this one. If you start with a min depth > 1 a vertex that was found before min depth might not be returned at all (it still might be part of a path). It is required to set order: "bfs" or order: "weighted" because with depth-first search the results would be unpredictable. Note: Using this configuration the result is not deterministic any more. If there are multiple paths from startVertex to vertex, one of those is picked. In case of a weighted traversal, the path with the lowest weight is picked, but in case of equal weights it is undefined which one is chosen.
    • "none" (default) – no uniqueness check is applied on vertices
  • uniqueEdges (string): optionally ensure edge uniqueness
    • "path" (default) – it is guaranteed that there is no path returned with a duplicate edge
    • "none" – no uniqueness check is applied on edges. Note: Using this configuration the traversal will follow edges in cycles.
  • edgeCollections (string|array): Optionally restrict edge collections the traversal may visit (introduced in v3.7.0). If omitted, or an empty array is specified, then there are no restrictions.
    • A string parameter is treated as the equivalent of an array with a single element.
    • Each element of the array should be a string containing the name of an edge collection.
  • vertexCollections (string|array): Optionally restrict vertex collections the traversal may visit (introduced in v3.7.0). If omitted, or an empty array is specified, then there are no restrictions.
    • A string parameter is treated as the equivalent of an array with a single element.
    • Each element of the array should be a string containing the name of a vertex collection.
    • The starting vertex is always allowed, even if it does not belong to one of the collections specified by a restriction.

  • parallelism (number, optional): Optionally parallelize traversal execution (introduced in v3.7.1). If omitted or set to a value of 1, traversal execution is not parallelized. If set to a value greater than 1, then up to that many worker threads can be used for concurrently executing the traversal. The value is capped by the number of available cores on the target machine.

    Parallelizing a traversal is normally useful when there are many inputs (start vertices) that the nested traversal can work on concurrently. This is often the case when a nested traversal is fed with several tens of thousands of start vertices, which can then be distributed randomly to worker threads for parallel execution.

    Traversal parallelization is only available in the Enterprise Edition, and limited to traversals in single server deployments and to cluster traversals that are running in a OneShard setup. Cluster traversals that run on a Coordinator node and SmartGraph traversals are currently not parallelized, even if the options is specified.

  • weightAttribute (string, optional): Specifies the name of an attribute that is used to look up the weight of an edge. If no attribute is specified or if it is not present in the edge document then the defaultWeight is used. The attribute value must not be negative.
  • defaultWeight (number, optional): Specifies the default weight of an edge. The value must not be negative. The default value is 1.

Working with collection sets

[WITH vertexCollection1[, vertexCollection2[, ...vertexCollectionN]]]
FOR vertex[, edge[, path]]
  IN [min[..max]]
  OUTBOUND|INBOUND|ANY startVertex
  edgeCollection1, ..., edgeCollectionN
  [PRUNE pruneCondition]
  [OPTIONS options]

Instead of GRAPH graphName you may specify a list of edge collections. Vertex collections are determined by the edges in the edge collections. The traversal options are the same as with the named graph variant, though the edgeCollections restriction option is redundant in this case.

If the same edge collection is specified multiple times, it will behave as if it were specified only once. Specifying the same edge collection is only allowed when the collections do not have conflicting traversal directions.

ArangoSearch Views cannot be used as edge collections.

Traversing in mixed directions

For traversals with a list of edge collections you can optionally specify the direction for some of the edge collections. Say for example you have three edge collections edges1, edges2 and edges3, where in edges2 the direction has no relevance but in edges1 and edges3 the direction should be taken into account. In this case you can use OUTBOUND as general traversal direction and ANY specifically for edges2 as follows:

FOR vertex IN OUTBOUND
  startVertex
  edges1, ANY edges2, edges3

All collections in the list that do not specify their own direction will use the direction defined after IN. This allows to use a different direction for each collection in your traversal.

Graph traversals in a cluster

Due to the nature of graphs, edges may reference vertices from arbitrary collections. Following the paths can thus involve documents from various collections and it is not possible to predict which will be visited in a traversal. Which collections need to be loaded by the graph engine can only be determined at run time.

Use the WITH statement to specify the collections you expect to be involved. This is required for traversals using collection sets in cluster deployments.

Using filters and the explainer to extrapolate the costs

All three variables emitted by the traversals might as well be used in filter statements. For some of these filter statements the optimizer can detect that it is possible to prune paths of traversals earlier, hence filtered results will not be emitted to the variables in the first place. This may significantly improve the performance of your query. Whenever a filter is not fulfilled, the complete set of vertex, edge and path will be skipped. All paths with a length greater than max will never be computed.

In the current state, AND combined filters can be optimized, but OR combined filters cannot.

The following examples are based on the traversal graph.

Pruning

Introduced in: v3.4.5

Pruning is the easiest variant to formulate conditions to reduce the amount of data to be checked during a search. So it allows to improve query performance and reduces the amount of overhead generated by the query.

You can use the vertex, edge, and path variables emitted by the traversal in a prune expression, as well as all other variables defined before the FOR operation.

Examples:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      PRUNE e.theTruth == true
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[
  {
    "vertices": [
      "A",
      "B"
    ],
    "edges": [
      "left_bar"
    ]
  },
  {
    "vertices": [
      "A",
      "G"
    ],
    "edges": [
      "right_foo"
    ]
  }
]

This will search until it sees an edge having theTruth == true. The path with this edge will be returned, the search will not continue after this edge. Namely all responses either have no edge with theTruth == true or the last edge on the path has theTruth == true.

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      PRUNE v._key == 'G'
      FILTER v._key == 'G'
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[
  {
    "vertices": [
      "A",
      "G"
    ],
    "edges": [
      "right_foo"
    ]
  }
]

This will search for all paths from the source circles/A to the vertex circles/G. This is done with first the PRUNE which makes sure we stop search as soon as we have found G and we will not go beyond G and via a loop return to it. With the second filter, we remove all paths that do not end in G namely all shorter ones that have not been cut out by prune. Hence the list of all paths from A to G are returned.

Note you can also prune as soon as you reach a certain collection with the following example:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      PRUNE IS_SAME_COLLECTION('circles', v)
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[]

There is also the option to store the PRUNE condition as a variable, as in the following example:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      PRUNE pruneCondition = v._key == 'G'
      FILTER pruneCondition
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[
  {
    "vertices": [
      "A",
      "G"
    ],
    "edges": [
      "right_foo"
    ]
  }
]

This will store the PRUNE condition v._key == 'G' in the variable pruneCondition. Later on, it will be used as the condition for FILTER to avoid retyping the condition that is the same as in PRUNE.

Filtering on paths

Filtering on paths allows for the second most powerful filtering and may have the second highest impact on performance. Using the path variable you can filter on specific iteration depths. You can filter for absolute positions in the path by specifying a positive number (which then qualifies for the optimizations), or relative positions to the end of the path by specifying a negative number.

Filtering edges on the path

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.edges[0].theTruth == true
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[
  {
    "vertices": [
      "A",
      "B"
    ],
    "edges": [
      "left_bar"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "C"
    ],
    "edges": [
      "left_bar",
      "left_blarg"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "C",
      "D"
    ],
    "edges": [
      "left_bar",
      "left_blarg",
      "left_blorg"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "E"
    ],
    "edges": [
      "left_bar",
      "left_blub"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "E",
      "F"
    ],
    "edges": [
      "left_bar",
      "left_blub",
      "left_schubi"
    ]
  },
  {
    "vertices": [
      "A",
      "G"
    ],
    "edges": [
      "right_foo"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H"
    ],
    "edges": [
      "right_foo",
      "right_blob"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H",
      "I"
    ],
    "edges": [
      "right_foo",
      "right_blob",
      "right_blub"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J"
    ],
    "edges": [
      "right_foo",
      "right_zip"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J",
      "K"
    ],
    "edges": [
      "right_foo",
      "right_zip",
      "right_zup"
    ]
  }
]

will filter all paths where the start edge (index 0) has the attribute theTruth equal to true. The resulting paths will be up to 5 items long.

Filtering vertices on the path

Similar to filtering the edges on the path you can also filter the vertices:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.vertices[1]._key == "G"
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[
  {
    "vertices": [
      "A",
      "G"
    ],
    "edges": [
      "right_foo"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H"
    ],
    "edges": [
      "right_foo",
      "right_blob"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H",
      "I"
    ],
    "edges": [
      "right_foo",
      "right_blob",
      "right_blub"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J"
    ],
    "edges": [
      "right_foo",
      "right_zip"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J",
      "K"
    ],
    "edges": [
      "right_foo",
      "right_zip",
      "right_zup"
    ]
  }
]

Combining several filters

And of course you can combine these filters in any way you like:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.edges[0].theTruth == true
         AND p.edges[1].theFalse == false
      FILTER p.vertices[1]._key == "G"
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[
  {
    "vertices": [
      "A",
      "G",
      "H"
    ],
    "edges": [
      "right_foo",
      "right_blob"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H",
      "I"
    ],
    "edges": [
      "right_foo",
      "right_blob",
      "right_blub"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J"
    ],
    "edges": [
      "right_foo",
      "right_zip"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J",
      "K"
    ],
    "edges": [
      "right_foo",
      "right_zip",
      "right_zup"
    ]
  }
]

The query will filter all paths where the first edge has the attribute theTruth equal to true, the first vertex is “G” and the second edge has the attribute theFalse equal to false. The resulting paths will be up to 5 items long.

Note: Although we have defined a min of 1, we will only get results of depth 2. This is because for all results in depth 1 the second edge does not exist and hence cannot fulfill the condition here.

Filter on the entire path

With the help of array comparison operators filters can also be defined on the entire path, like ALL edges should have theTruth == true:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.edges[*].theTruth ALL == true
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[
  {
    "vertices": [
      "A",
      "B"
    ],
    "edges": [
      "left_bar"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "C"
    ],
    "edges": [
      "left_bar",
      "left_blarg"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "C",
      "D"
    ],
    "edges": [
      "left_bar",
      "left_blarg",
      "left_blorg"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "E"
    ],
    "edges": [
      "left_bar",
      "left_blub"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "E",
      "F"
    ],
    "edges": [
      "left_bar",
      "left_blub",
      "left_schubi"
    ]
  },
  {
    "vertices": [
      "A",
      "G"
    ],
    "edges": [
      "right_foo"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H"
    ],
    "edges": [
      "right_foo",
      "right_blob"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H",
      "I"
    ],
    "edges": [
      "right_foo",
      "right_blob",
      "right_blub"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J"
    ],
    "edges": [
      "right_foo",
      "right_zip"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J",
      "K"
    ],
    "edges": [
      "right_foo",
      "right_zip",
      "right_zup"
    ]
  }
]

Or NONE of the edges should have theTruth == true:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.edges[*].theTruth NONE == true
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[]

Both examples above are recognized by the optimizer and can potentially use other indexes than the edge index.

It is also possible to define that at least one edge on the path has to fulfill the condition:

FOR v, e, p IN 1..5 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.edges[*].theTruth ANY == true
      RETURN { vertices: p.vertices[*]._key, edges: p.edges[*].label }

[
  {
    "vertices": [
      "A",
      "B"
    ],
    "edges": [
      "left_bar"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "C"
    ],
    "edges": [
      "left_bar",
      "left_blarg"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "C",
      "D"
    ],
    "edges": [
      "left_bar",
      "left_blarg",
      "left_blorg"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "E"
    ],
    "edges": [
      "left_bar",
      "left_blub"
    ]
  },
  {
    "vertices": [
      "A",
      "B",
      "E",
      "F"
    ],
    "edges": [
      "left_bar",
      "left_blub",
      "left_schubi"
    ]
  },
  {
    "vertices": [
      "A",
      "G"
    ],
    "edges": [
      "right_foo"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H"
    ],
    "edges": [
      "right_foo",
      "right_blob"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "H",
      "I"
    ],
    "edges": [
      "right_foo",
      "right_blob",
      "right_blub"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J"
    ],
    "edges": [
      "right_foo",
      "right_zip"
    ]
  },
  {
    "vertices": [
      "A",
      "G",
      "J",
      "K"
    ],
    "edges": [
      "right_foo",
      "right_zip",
      "right_zup"
    ]
  }
]

It is guaranteed that at least one, but potentially more edges fulfill the condition. All of the above filters can be defined on vertices in the exact same way.

Filtering on the path vs. filtering on vertices or edges

Filtering on the path influences the Iteration on your graph. If certain conditions aren’t met, the traversal may stop continuing along this path.

In contrast filters on vertex or edge only express whether you’re interested in the actual value of these documents. Thus, it influences the list of returned documents (if you return v or e) similar as specifying a non-null min value. If you specify a min value of 2, the traversal over the first two nodes of these paths has to be executed - you just won’t see them in your result array.

Similar are filters on vertices or edges - the traverser has to walk along these nodes, since you may be interested in documents further down the path.

Examples

We will create a simple symmetric traversal demonstration graph:

arangosh> var examples = require("@arangodb/graph-examples/example-graph.js");
arangosh> var graph = examples.loadGraph("traversalGraph");
arangosh> db.circles.toArray();
arangosh> db.edges.toArray();
arangosh> print("once you don't need them anymore, clean them up:");
arangosh> examples.dropGraph("traversalGraph");

[ 
  { 
    "_key" : "A", 
    "_id" : "circles/A", 
    "_rev" : "_gjDAjG6---", 
    "label" : "1" 
  }, 
  { 
    "_key" : "B", 
    "_id" : "circles/B", 
    "_rev" : "_gjDAjG6--_", 
    "label" : "2" 
  }, 
  { 
    "_key" : "C", 
    "_id" : "circles/C", 
    "_rev" : "_gjDAjG6--A", 
    "label" : "3" 
  }, 
  { 
    "_key" : "D", 
    "_id" : "circles/D", 
    "_rev" : "_gjDAjG6--B", 
    "label" : "4" 
  }, 
  { 
    "_key" : "E", 
    "_id" : "circles/E", 
    "_rev" : "_gjDAjG6--C", 
    "label" : "5" 
  }, 
  { 
    "_key" : "F", 
    "_id" : "circles/F", 
    "_rev" : "_gjDAjG6--D", 
    "label" : "6" 
  }, 
  { 
    "_key" : "G", 
    "_id" : "circles/G", 
    "_rev" : "_gjDAjH----", 
    "label" : "7" 
  }, 
  { 
    "_key" : "H", 
    "_id" : "circles/H", 
    "_rev" : "_gjDAjH---_", 
    "label" : "8" 
  }, 
  { 
    "_key" : "I", 
    "_id" : "circles/I", 
    "_rev" : "_gjDAjH---A", 
    "label" : "9" 
  }, 
  { 
    "_key" : "J", 
    "_id" : "circles/J", 
    "_rev" : "_gjDAjH---B", 
    "label" : "10" 
  }, 
  { 
    "_key" : "K", 
    "_id" : "circles/K", 
    "_rev" : "_gjDAjH---C", 
    "label" : "11" 
  } 
]
[ 
  { 
    "_key" : "63206", 
    "_id" : "edges/63206", 
    "_from" : "circles/A", 
    "_to" : "circles/B", 
    "_rev" : "_gjDAjH---D", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_bar" 
  }, 
  { 
    "_key" : "63208", 
    "_id" : "edges/63208", 
    "_from" : "circles/B", 
    "_to" : "circles/C", 
    "_rev" : "_gjDAjH---E", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blarg" 
  }, 
  { 
    "_key" : "63210", 
    "_id" : "edges/63210", 
    "_from" : "circles/C", 
    "_to" : "circles/D", 
    "_rev" : "_gjDAjH---F", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blorg" 
  }, 
  { 
    "_key" : "63212", 
    "_id" : "edges/63212", 
    "_from" : "circles/B", 
    "_to" : "circles/E", 
    "_rev" : "_gjDAjH---G", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_blub" 
  }, 
  { 
    "_key" : "63214", 
    "_id" : "edges/63214", 
    "_from" : "circles/E", 
    "_to" : "circles/F", 
    "_rev" : "_gjDAjHC---", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "left_schubi" 
  }, 
  { 
    "_key" : "63216", 
    "_id" : "edges/63216", 
    "_from" : "circles/A", 
    "_to" : "circles/G", 
    "_rev" : "_gjDAjHC--_", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_foo" 
  }, 
  { 
    "_key" : "63218", 
    "_id" : "edges/63218", 
    "_from" : "circles/G", 
    "_to" : "circles/H", 
    "_rev" : "_gjDAjHC--A", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_blob" 
  }, 
  { 
    "_key" : "63220", 
    "_id" : "edges/63220", 
    "_from" : "circles/H", 
    "_to" : "circles/I", 
    "_rev" : "_gjDAjHC--B", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_blub" 
  }, 
  { 
    "_key" : "63222", 
    "_id" : "edges/63222", 
    "_from" : "circles/G", 
    "_to" : "circles/J", 
    "_rev" : "_gjDAjHC--C", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_zip" 
  }, 
  { 
    "_key" : "63224", 
    "_id" : "edges/63224", 
    "_from" : "circles/J", 
    "_to" : "circles/K", 
    "_rev" : "_gjDAjHC--D", 
    "theFalse" : false, 
    "theTruth" : true, 
    "label" : "right_zup" 
  } 
]
once you don't need them anymore, clean them up:

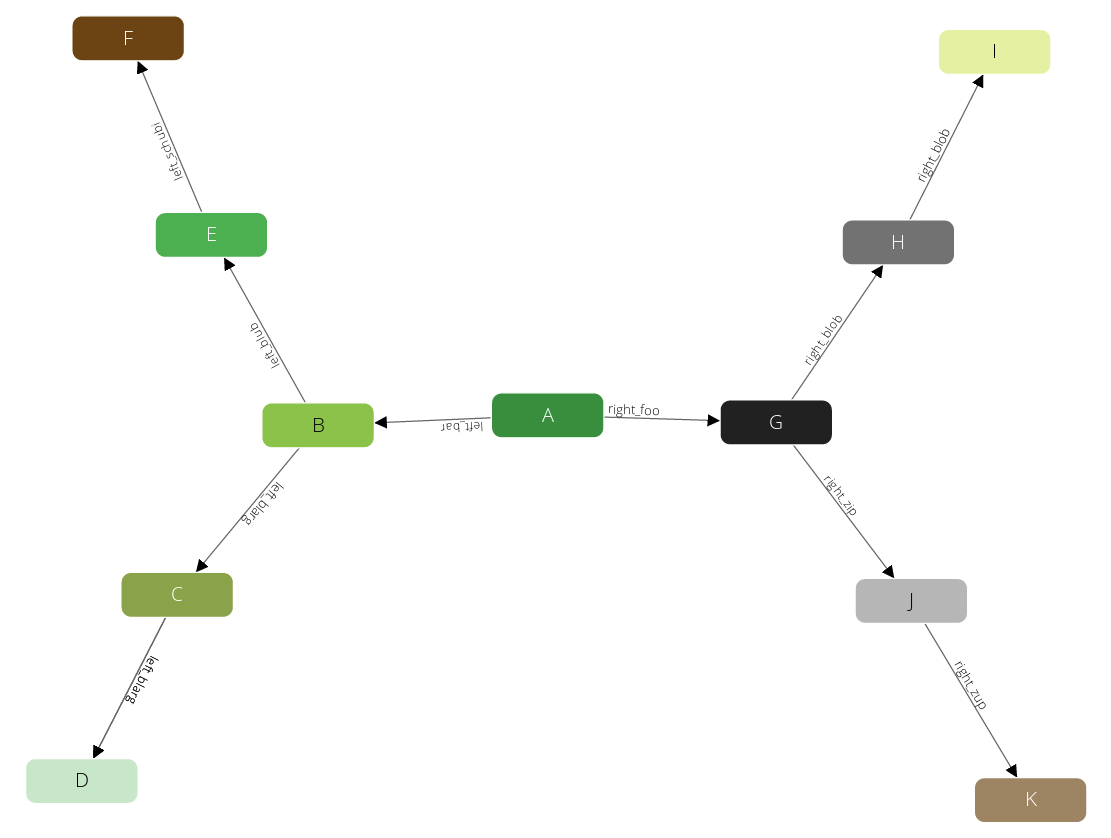
To get started we select the full graph. For better overview we only return the vertex IDs:

FOR v IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
    RETURN v._key

[
  "B",
  "C",
  "D",
  "E",
  "F",
  "G",
  "H",
  "I",
  "J",
  "K"
]

FOR v IN 1..3 OUTBOUND 'circles/A' edges RETURN v._key

[
  "B",
  "C",
  "D",
  "E",
  "F",
  "G",
  "H",
  "I",
  "J",
  "K"
]

We can nicely see that it is heading for the first outer vertex, then goes back to the branch to descend into the next tree. After that it returns to our start node, to descend again. As we can see both queries return the same result, the first one uses the named graph, the second uses the edge collections directly.

Now we only want the elements of a specific depth (min = max = 2), the ones that are right behind the fork:

FOR v IN 2..2 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
    RETURN v._key

[
  "C",
  "E",
  "H",
  "J"
]

FOR v IN 2 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
    RETURN v._key

[
  "C",
  "E",
  "H",
  "J"
]

As you can see, we can express this in two ways: with or without max parameter in the expression.

Filter examples

Now let’s start to add some filters. We want to cut of the branch on the right side of the graph, we may filter in two ways:

• we know the vertex at depth 1 has _key == G
• we know the label attribute of the edge connecting A to G is right_foo

FOR v, e, p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.vertices[1]._key != 'G'
      RETURN v._key

[
  "B",
  "C",
  "D",
  "E",
  "F"
]

FOR v, e, p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.edges[0].label != 'right_foo'
      RETURN v._key

[
  "B",
  "C",
  "D",
  "E",
  "F"
]

As we can see all vertices behind G are skipped in both queries. The first filters on the vertex _key, the second on an edge label. Note again, as soon as a filter is not fulfilled for any of the three elements v, e or p, the complete set of these will be excluded from the result.

We also may combine several filters, for instance to filter out the right branch (G), and the E branch:

FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.vertices[1]._key != 'G'
      FILTER p.edges[1].label != 'left_blub'
      RETURN v._key

[
  "B",
  "C",
  "D"
]

FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.vertices[1]._key != 'G' AND p.edges[1].label != 'left_blub'
      RETURN v._key

[
  "B",
  "C",
  "D"
]

As you can see, combining two FILTER statements with an AND has the same result.

Comparing OUTBOUND / INBOUND / ANY

All our previous examples traversed the graph in OUTBOUND edge direction. You may however want to also traverse in reverse direction (INBOUND) or both (ANY). Since circles/A only has outbound edges, we start our queries from circles/E:

FOR v IN 1..3 OUTBOUND 'circles/E' GRAPH 'traversalGraph'
      RETURN v._key

[
  "F"
]

FOR v IN 1..3 INBOUND 'circles/E' GRAPH 'traversalGraph'
      RETURN v._key

[
  "B",
  "A"
]

FOR v IN 1..3 ANY 'circles/E' GRAPH 'traversalGraph'
      RETURN v._key

[
  "F",
  "B",
  "C",
  "D",
  "A",
  "G"
]

The first traversal will only walk in the forward (OUTBOUND) direction. Therefore from E we only can see F. Walking in reverse direction (INBOUND), we see the path to A: B → A.

Walking in forward and reverse direction (ANY) we can see a more diverse result. First of all, we see the simple paths to F and A. However, these vertices have edges in other directions and they will be traversed.

Note: The traverser may use identical edges multiple times. For instance, if it walks from E to F, it will continue to walk from F to E using the same edge once again. Due to this we will see duplicate nodes in the result.

Please note that the direction can’t be passed in by a bind parameter.

Use the AQL explainer for optimizations

Now let’s have a look what the optimizer does behind the curtain and inspect traversal queries using the explainer:

FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      LET localScopeVar = RAND() > 0.5
      FILTER p.edges[0].theTruth != localScopeVar
      RETURN v._key

Query String (173 chars, cacheable: false):
   FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
       LET localScopeVar = RAND() > 0.5
       FILTER p.edges[0].theTruth != localScopeVar
       RETURN v._key
 

Execution plan:
 Id   NodeType          Est.   Comment
  1   SingletonNode        1   * ROOT
  2   TraversalNode        1     - FOR v  /* vertex */, p  /* paths: edges */ IN 1..3  /* min..maxPathDepth */ OUTBOUND 'circles/A' /* startnode */  GRAPH 'traversalGraph'
  3   CalculationNode      1       - LET localScopeVar = (RAND() > 0.5)   /* simple expression */
  4   CalculationNode      1       - LET #6 = (p.`edges`[0].`theTruth` != localScopeVar)   /* simple expression */
  5   FilterNode           1       - FILTER #6
  6   CalculationNode      1       - LET #8 = v.`_key`   /* attribute expression */
  7   ReturnNode           1       - RETURN #8

Indexes used:
 By   Name   Type   Collection   Unique   Sparse   Selectivity   Fields        Ranges
  2   edge   edge   edges        false    false       100.00 %   [ `_from` ]   base OUTBOUND

Functions used:
 Name   Deterministic   Cacheable   Uses V8
 RAND   false           false       false  

Traversals on graphs:
 Id  Depth  Vertex collections  Edge collections  Options                                  Filter / Prune Conditions
 2   1..3   circles             edges             uniqueVertices: none, uniqueEdges: path                           

Optimization rules applied:
 Id   RuleName
  1   move-calculations-up
  2   optimize-traversals
  3   remove-redundant-path-var
  4   move-calculations-down

Optimization rules with highest execution times:
 RuleName                                    Duration [s]
 optimize-subqueries                              0.00002
 optimize-traversals                              0.00001
 move-calculations-up                             0.00001
 remove-filter-covered-by-traversal               0.00000
 remove-redundant-calculations                    0.00000

41 rule(s) executed, 1 plan(s) created

FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
      FILTER p.edges[0].label == 'right_foo'
      RETURN v._key

Query String (129 chars, cacheable: true):
   FOR v,e,p IN 1..3 OUTBOUND 'circles/A' GRAPH 'traversalGraph'
       FILTER p.edges[0].label == 'right_foo'
       RETURN v._key
 

Execution plan:
 Id   NodeType          Est.   Comment
  1   SingletonNode        1   * ROOT
  2   TraversalNode        1     - FOR v  /* vertex */ IN 1..3  /* min..maxPathDepth */ OUTBOUND 'circles/A' /* startnode */  GRAPH 'traversalGraph'
  5   CalculationNode      1       - LET #7 = v.`_key`   /* attribute expression */
  6   ReturnNode           1       - RETURN #7

Indexes used:
 By   Name   Type   Collection   Unique   Sparse   Selectivity   Fields        Ranges
  2   edge   edge   edges        false    false       100.00 %   [ `_from` ]   base OUTBOUND
  2   edge   edge   edges        false    false       100.00 %   [ `_from` ]   level 0 OUTBOUND

Traversals on graphs:
 Id  Depth  Vertex collections  Edge collections  Options                                  Filter / Prune Conditions                   
 2   1..3   circles             edges             uniqueVertices: none, uniqueEdges: path  FILTER (p.`edges`[0].`label` == "right_foo")

Optimization rules applied:
 Id   RuleName
  1   move-calculations-up
  2   move-filters-up
  3   move-calculations-up-2
  4   move-filters-up-2
  5   optimize-traversals
  6   remove-filter-covered-by-traversal
  7   remove-unnecessary-calculations-2
  8   remove-redundant-path-var

Optimization rules with highest execution times:
 RuleName                                    Duration [s]
 optimize-traversals                              0.00001
 remove-filter-covered-by-traversal               0.00001
 move-calculations-up                             0.00000
 move-calculations-up-2                           0.00000
 move-filters-up                                  0.00000

42 rule(s) executed, 1 plan(s) created

We now see two queries: In one we add a variable localScopeVar, which is outside the scope of the traversal itself - it is not known inside of the traverser. Therefore, this filter can only be executed after the traversal, which may be undesired in large graphs. The second query on the other hand only operates on the path, and therefore this condition can be used during the execution of the traversal. Paths that are filtered out by this condition won’t be processed at all.

And finally clean it up again:

arangosh> var examples = require("@arangodb/graph-examples/example-graph.js");
arangosh> examples.dropGraph("traversalGraph");

(Empty output)

If this traversal is not powerful enough for your needs, like you cannot describe your conditions as AQL filter statements, then you might want to have a look at manually crafted traversers.

Also see how to combine graph traversals.